7 .Пример: "Открытие" второго закона Ньютона.
Рассмотрим задачу определения по результатам наблюдений зависимости между ускорением тела, его массой и действующей на тело силой ( закона Ньютона ). Вектор наблюдаемых параметров Y, характеризующих изучаемое явление, будем считать состоящим из четырех элементов: y1 = m и y2 = a - соответственно массы и ускорения тела, y3 - случайно попавшей в поле зрения исследователя величины, не имеющей отношения к анализируемой ситуации ( помехи ), и y4 = F - действующей на тело силы.
Вектор X характеризующих исследуемое явление параметров в рассматриваемом случае содержит три координаты: x1 = m, x2 = a, x3 = F . Соотношения между составляющими векторов y и x определяются, таким образом, следующими зависимостями :
Степень аппроксимирующего полинома зададим равной двум. Число столбцов матрицы A в нашем случае будет равно четырем, матрицы D - пятнадцати. Параметрам y1 - y3 при моделировании будем придавать случайные независимые между собой значения. Величина y4 , естественно, всегда будет равна произведению y1 на y2 . Вносимые в процессе измерения ошибки будем менять в пределах от нуля до пяти процентов от измеряемых величин.
Результаты оценки по 100 реализациям значений вторых начальных моментов определителя матрицы D при различных уровнях ошибок измерения (первая строка), а также этих моментов после замены столбцов матриц A (второй блок таблицы) и D (третий блок) столбцами с элементами, распределенными в соответствии с теми же законами, но независимыми от элементов столбцов исходных матриц, приведены в таблице 2.

Приведенные числовые результаты показывают, что четыре наблюдаемых параметра y1 , y2 , y3 и y4 связаны между собой только одной зависимостью ( ранг матрицы D, состоящей из 15 строк и 15 столбцов, равен 14 ) и что среди столбцов матрицы D есть только два линейно зависимых ( r = 2 ) : с номерами 4 и 6. Им соответствуют две системы линейных неоднородных уравнений (7), которые имеют решения :
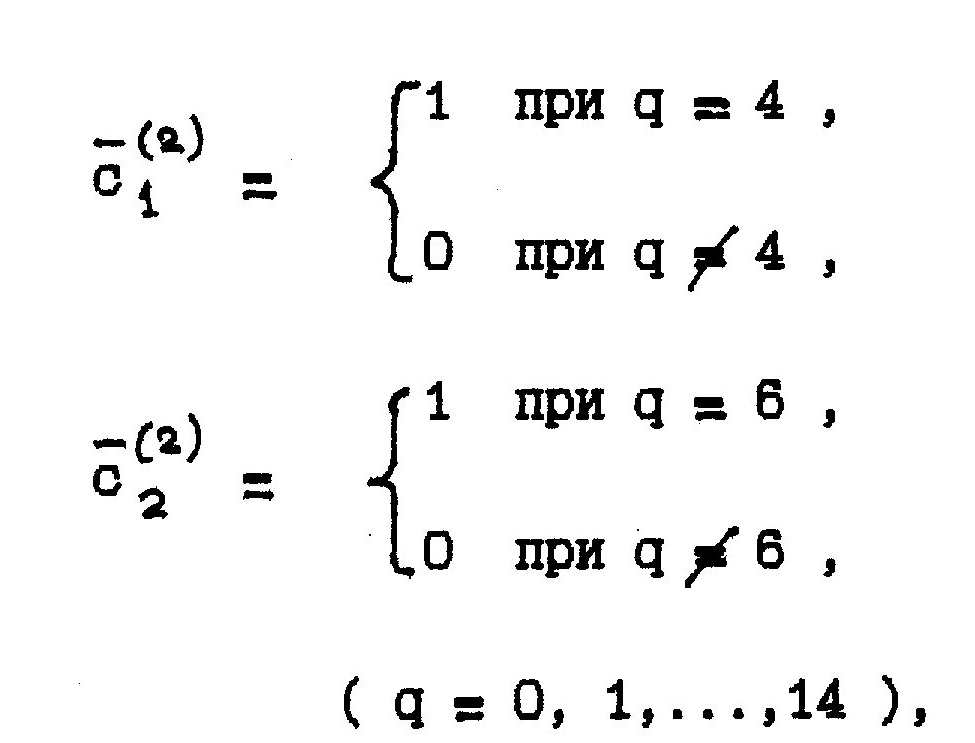
определяющие одну и ту же зависимость между элементами столбцов матрицы D :
что соответствует зависимости между характеризующими явление параметрами xi ( i = 1, 2, 3) :
Заметим, что размерность задачи до решения систем уравнений (до этапа
решения задачи регрессионного анализа) могла быть снижена: столбец
a3 матрицы A и все столбцы матрицы
D, кроме d4 и
d6 , можно было удалить и тем самым
упростить задачу.
Несколько расширим задачу, включив в число наблюдаемых величин параметры, характеризующие движение тела массы m под действием силы F : его положение и скорость в два момента времени to и t .
Вектор наблюдаемых параметров при этом кроме y1
- y4 будет включать еще следующие
элементы :
y5 = X0 , y6 = V0 -
начальные значения положения и скорости тела в момент времени
to , y7 = X ,
y8 = V - значения положения и скорости в момент
t , y9 = t0 ,
y10 = t .
Число столбцов матрицы A теперь будет равно 10-и, а матрицы D при степени аппроксимирующего полинома равной трем - 286-и. Элементы столбцов матрицы D в рассматриваемом случае оказываются связанными между собой ткими тремя соотношениями:
Число столбцов матрицы A теперь будет равно 10-и, а матрицы D при степени аппроксимирующего полинома равной трем - 286-и. Элементы столбцов матрицы D в рассматриваемом случае оказываются связанными между собой ткими тремя соотношениями:

Кроме этих между элементами столбцов матрицы D существуют еще "вторичные" зависимости. Все они тождественны соотношениям (9).