8. Пример:"Доказательство" теоремы Пифагора

Теорема Пифагора в геометрических терминах формулируется следующим образом:

Эту теорему можно сформулировать, используя алгебраическую форму записи :

где a,b – катеты прямоугольного треугольника, а c – его гипотенуза.

Впервые с доказательством теоремы Пифагора мы сталкиваемся в средней школе . В статье “Теорема Пифагора”(Материал из Википедии — свободной энциклопедии) сказано, что на данный момент в научной литературе зафиксировано 367 доказательств этой теоремы. Известны доказательства Евклида, Леонардо да Винчи, самого Пифагора. В них используются самые разнообразные подходы : геометрический ( через подобные треугольники , с помощью метода площадей), основанный на анализе бесконечно малых , векторный и т.д. и т.д.

Справедливость выражения (1) может быть доказана также с помощью метода, основанного на анализе результатов наблюдений ( измерений ) параметров , характеризующих изучаемое явление, и выявлении скрытых в этих результатах зависимостей между параметрами (См.разд 1-9).

Наблюдаемыми параметрами в нашем случае являются: длина катетов a и b и гипотенузы c прямоугольного треугольника , а интересующая нас скрытая в этих данных зависимость - соотношение между величинами a, b и c.

Интересующие нас зависимости могут быть достаточно просто установлены тогда, когда они представляют собой полином степени p относительно своих параметров. Используемую формулу представления зависимости между параметрами исследуемой зависимости в виде полинома можно посмотреть в разделе 2. Число членов этого полинома K зависит от числа параметров функции M и степени полинома p .

Решение задачи прямоугольного треугольника предусматривает выполнение следующих трёх этапов.

1. 1.  Формирования матрицы наблюдений A[ i , j ] = | a [ i,j ] |  ( i = 1, , M ; j = 1, .. , N ) , где N – число экспериментов. Элементы этой матрицы a[i,j] представляют собой измеренные в j– том эксперименте i – того параметра.
2. 2.  Формирования матрицы D[i,j]  ( i = 0, 1,.., K ; j = 1,.., N ) . Элементы матрицы d[i,j] определяются на основании элементов матрицы A[ i , j ] в соответствии с формулой представления зависимости между параметрами исследуемой зависимости.
3. 3.  Проверка существования линейной зависимости между столбцами матрицы D[i,j] ; решение системы линейных алгебраических уравнений и определение зависимости между параметрами.

Матрица A[i,j] ( i = 1, , M ; j = 1, .. , N ) может быть заполнена данными, полученными в результате измерения длинны катетов a[j],b[j] и гипотенузы с[j] ( j = 1, .. , N ) N разных прямоугольных треугольников. В нашем эксперименте будем придавать величинам a[j] и b[j] независимые положительные случайные значения, а с[j] определять в соответствии с формулой :

В состав матрицы A[i,j], кроме столбцов , содержащих значения a, b и с, включим ещё один столбец, элементы которого независимы от a и b и выступают в роли помехи.

Матрица результатов измерений A[i,j] , таким образом, имеет следующий вид : первые два столбца - это измеренные значения катетов прямоугольных треугольников

третий столбец a[j,3] - независимые от a[j,1] и a[j,2] случайные помехи, а четвёртый a[j,4] – их гипотенузы (j=1,..,N).

Число строк матрицы результатов измерений A[i,j] (число измерений N ) должно быть выбрано равным числу столбцов матрицы D[i,j] K. В нашем случае при числе столбцов матрицы A[i,j] М=4 и степени полинома p=2 число столбцов матрицы D[i,j] K = 15. Соответственно N = 15.

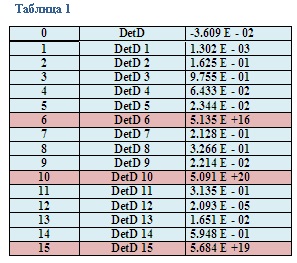
Результаты проверки на основании критерия существования линейной зависимости между параметрами исследуемого явления приведены в Таблице 1.

В нулевой строке таблицы приведено значение определителя матрицы D[i,j]. Оно не равно нулю ( хотя линейная зависимость между её столбцами есть) из-за искусственно введённых ошибок измерения параметров a, b и c.

В строках от первой до пятнадцатой приведены значения определителей этой матрицы после искусственного разрыва причинно-следственных связей между её столбцами, который осуществлялся заменой значений элементов i-того столбца ( i=1.2….15 ) независимыми случайными значениями с таким же, как и у исходного столбца, законом распределения.

Приведенные результаты показывают, что между столбцами матрицы D[i,j] существует только одна линейная зависимость. и в этой зависимости участвуют столбцы № 6,10 и 15 (Выделены розовым цветом). Этим столбцам соответствуют члены разложения соответственно : a[1]2, a[2]2 и a[4]2.

Для определения зависимости между параметрами a, b и c необходимо решить систему N – 1 линейных алгебраических уравнений с матрицей размера (N–1)*(N–1), полученной из N*N матрицы D[i,j] вычеркиванием последнего столбца и последней строки и вектором свободных членов, полученным из последнего столбца матрицы D[i,j] удалением последнего элемента. Решение этой системы представлено в Таблице 2.

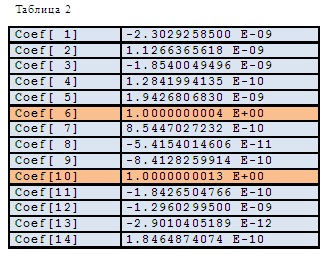
Результаты решения показывают, что коэффициенты разложения Сoef[ 6] и Сoef[ 10] при a[1]2 и a[2]2 равны 1, остальные – нулю. Что соответствует зависимости :

a[1]²+ a[2]²=a[4]²

Или, что то же самое:

a²+ b²=c²

© 2009-2015 ИП Щелкановцев. Все права защищены.