2. Основные обозначения, предварительные
преобразования
Предположим, что вид исследуемых функциональных зависимостей (1) известен. Неизвестными является только значения векторов параметров С .
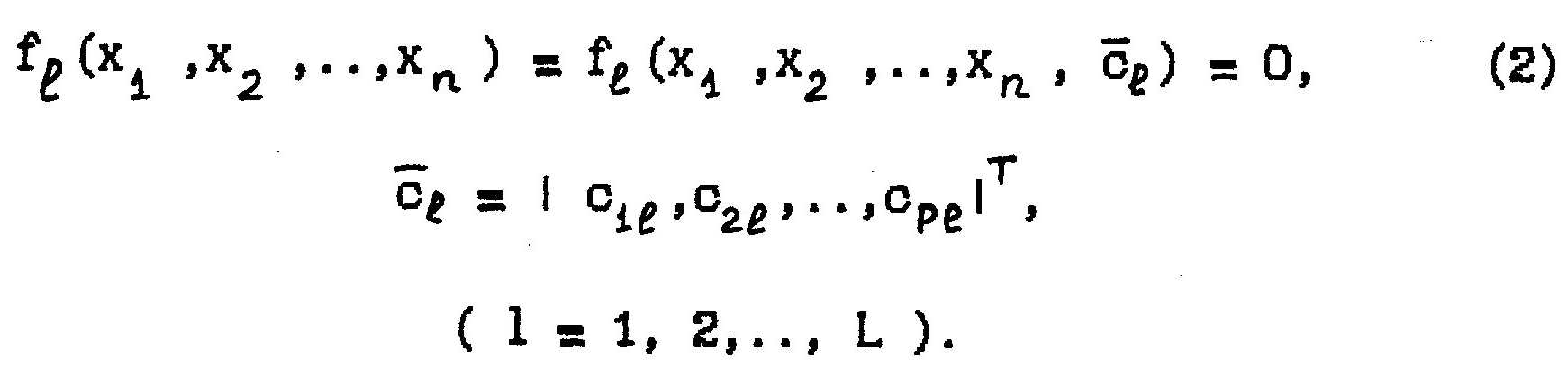
Многие гладкие функции могут быть представлены [3],[5] в виде алгебраического полинома относительно переменных:

содержащего свободный член, линейные, квадратичные и т.д. слагаемые. Число P членов полиномов (3) зависит от числа n параметров функций (1) и степени разложения этих функций в ряд. В дальнейшем будем считать, что все степени ml ( l = 1,..,L ) разложения функций (2) равны их максимальному значению m : m = Max ( m1,m2 ,..,mL). Представление функций отклика (1) в виде полинома (3), линейного относительно неизвестных параметров cq ( q = 1,2,..,P ) и нелинейного относительно аргументов xp ( p = 1,2,..,n ), удобно для решения задачи исследования зависимостей между параметрами, характеризующими природные явления. Оно позволяет использовать для решения задачи хорошо разработанный аппарат регрессионного и конфлюэнтного анализа [3],[6]. Удобство представления (3) объясняется также тем, что многие физические законы записываются с помощью соотношений, представляющих собой его частные случаи. Это свойство является следствием того, что функциональные зависимости, выражающие физические факты, не зависящие от единиц измерения, обладают специальной структурой. Особенности структуры соотношений, с помощью которых записываются физические закономерности, аналитически определяются формулой размерности, утверждающей , что размерности физических величин имеют вид степенных полиномов, а также вытекающей из этой формулы П-теоремы теории подобия [8],[9].
Введем в рассмотрение матрицу "D" размерности P * P :

Матрица D, аналогичная матрице плана в теории планирования экспериментов [6], обладает рядом полезных для нас свойств. Одно из них позволяет сформулировать критерий существования связи между параметрами исследуемого явления. Сформулируем его в виде Утверждения 1, справедливость которого легко может быть доказана.